寒假算法练习
week 1
今天是2021/1/15
然而写下这个的时候是2021/2/18
。。。。。懒人本懒了
递归实现指数型枚举
链接:https://ac.nowcoder.com/acm/problem/50911
来源:牛客网题目描述
从 1∼n1\sim n1∼n这 n (n≤16)(n \leq 16)(n≤16) 个整数中随机选取任意多个,输出所有可能的选择方案。
输入描述:
一个整数n。输出描述:
每行一种方案。同一行内的数必须升序排列,相邻两个数用恰好1个空格隔开。对于没有选任何数的方案,输出空行。本题有自定义校验器(SPJ),各行(不同方案)之间的顺序任意。示例1
输入
3输出
3 2 2 3 1 1 3 1 2 1 2 3
/*
_ooOoo_
o8888888o
88" . "88
(| -_- |)
O\ = /O
____/`---'\____
.' \\| |// `.
/ \\||| : |||// \
/ _||||| -:- |||||- \
| | \\\ - /// | |
| \_| ''\---/'' | |
\ .-\__ `-` ___/-. /
___`. .' /--.--\ `. . __
."" '< `.___\_<|>_/___.' >'"".
| | : `- \`.;`\ _ /`;.`/ - ` : | |
\ \ `-. \_ __\ /__ _/ .-` / /
======`-.____`-.___\_____/___.-`____.-'======
`=---='
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
佛祖保佑 永无BUG
@Author: xiaomu
@Time: 2021/2/18 8:13
@Project_NAME:_Algorithm_training
@FileName: NC50911.cpp
@IDE: CLion
*/
#include <cstdio>
#include <iostream>
using namespace std;
int pre[20];
int n;
void print(int len)
{
for(int i=0;i<len;i++)
{
printf("%d%c",pre[i],i==len-1?'\n':' ');
}
if(len==0)
puts(" ");
}//升序输出
void dfs(int pr,int dep)
{
for(int i =pr+1;i<=n;i++)
{
pre[dep]=i;
dfs(i,dep+1);
}
print(dep);
}
int main()
{
cin>>n;
dfs(0,0);
return 0;
}这道题目主要是为了考察了深度遍历树的建立
递归实现组合型枚举 ·
链接:https://ac.nowcoder.com/acm/problem/50918
来源:牛客网输入描述:
两个整数n,m。输出描述:
按照从小到大的顺序输出所有方案,每行1个。首先,同一行内的数升序排列,相邻两个数用一个空格隔开。其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面(例如1 3 9 12排在1 3 10 11前面)。输入
5 3输出
1 2 3 1 2 4 1 2 5 1 3 4 1 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5
#include <cstdio>
#include <iostream>
using namespace std;
int n,m;//n表示1-n,m表示行数;
int pre[20];
void print()
{
for (int i = 1; i <=m ; ++i) {
cout<<pre[i]<<' ';
}
cout<<'\n';
}
void dfs(int node,int deep)
{
if(deep<=m&&node<=n)
{ while(deep<=m&&node<=n)
{
pre[deep]=node;
dfs(node+1,deep+1);
if(deep==m) {
print();
}
node++;
}
}
else
return;
}
int main()
{
cin>>n>>m;
dfs(1,1);
return 0;
}这里考察递归栈的使用
第一个没看题解自己写出来的题目~开心
递归实现排列型枚举
链接:https://ac.nowcoder.com/acm/problem/50919
来源:牛客网题目描述
把 1∼n1\sim n1∼n 这 n(n<10)(n \lt 10)(n<10)个整数排成一行后随机打乱顺序,输出所有可能的次序。
输入描述:
一个整数n。输出描述:
按照从小到大的顺序输出所有方案,每行1个。 首先,同一行相邻两个数用一个空格隔开。其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面。示例1
输入
3输出
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1
#include<stdio.h>
int a[11],n,used[11];
void dfs(int dep)
{
int i;
if(dep == n + 1){ printf("%d",a[1]);
for(i = 2; i <= n; i++)
printf(" %d",a[i]); printf("\n");
return ;
}
for(i = 1; i <= n; i++)
if(!used[i]){
used[i] = 1, a[dep] = i;
dfs(dep + 1);
used[i] = 0;
}
}
int main()
{
scanf("%d",&n);
dfs(1);
return 0;
}这次的退栈比较巧妙
或者利用c++的排列数函数来计算
#include<iostream>
#include<algorithm>
using namespace std;
int a[15], n;
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
a[i] = i;//先按照升序对创建数组
do//先do否则输出不了123.....n
{
for(int i = 1; i <= n; i++)
cout << a[i] << ' ';
cout << endl;
}while(next_permutation(a + 1, a + n + 1));//求以ai开头的全排列
return 0;
}翻硬币
链接:https://ac.nowcoder.com/acm/problem/14355
来源:牛客网题目描述
小明正在玩一个“翻硬币”的游戏。
桌上放着排成一排的若干硬币。我们用 * 表示正面,用 o 表示反面(是小写字母,不是零)。
比如,可能情形是:*oo**oooo
如果同时翻转左边的两个硬币,则变为:oooo***oooo
现在小明的问题是:如果已知了初始状态和要达到的目标状态,每次只能同时翻转相邻的两个硬币,那么对特定的局面,最少要翻动多少次呢?
我们约定:把翻动相邻的两个硬币叫做一步操作,那么要求:
输入描述:
两行等长的字符串,分别表示初始状态和要达到的目标状态。每行的长度<1000输出描述:
一个整数,表示最小操作步数。示例1
输入
********** o****o****输出
5示例2
输入
*o**o***o*** *o***o**o***输出
1
#include <cstring>
#include <iostream>
using namespace std;
const int N =110;
int n;
char str1[N],str2[N];
void turn(int i)
{
if(str1[i]=='*')
str1[i]='o';
else
str1[i]='*';
}
int main()
{
cin>>str1>>str2;
n=strlen(str1);
int res=0;
for(int i=0;i<n-1;i++)
if(str1[i]!=str2[i])
{
turn(i),turn(i+1);
res++;
}
cout<<res;
return 0;
}这题用暴力搜素法来进行解题
先读入字符串1和2
当发现1和2有不同,立即翻1相邻两个硬币
带分数
链接:https://ac.nowcoder.com/acm/problem/14353
来源:牛客网题目描述
100 可以表示为带分数的形式:100 = 3 + 69258 / 714。
还可以表示为:100 = 82 + 3546 / 197。
注意特征:带分数中,数字1~9分别出现且只出现一次(不包含0)。
类似这样的带分数,100 有 11 种表示法。
输入描述:
从标准输入读入一个正整数N (N<1000*1000)输出描述:
程序首先输出正整数N,然后在输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数n。 注意:不要求输出每个表示,只统计有多少表示法! 输出格式:N n示例1
输入
100输出
100 11示例2
输入
105输出
105 6
这题也是暴力搜索法解
思路:
先对1-9进行全排列
然后对1-9进行分割和组合,然后暴力搜索能否符合和为目标数
#include<iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int asw=0;
int flag[10],a[10];
int sum(int start,int end)//字符串变成数字
{
int i,sum=0;
for(i=start;i<end;i++)
sum=sum*10+a[i+1];
return sum;
}
void Found(int a[],int n,int m)
{
int i,j,begin=0;
//开始裁缝分数组
//吧全排列好的数组分别划分成整数,分子,分母
for (int k = 1; k <n ; ++k) {
int m1=sum(0,i);//从1到9开始选择数
if(m1>=m) return;//如果第一个整数就比给定的数要大就直接淘汰
for (int j=i+(n-i)/2; j<n-1 ; ++j) {
int m2=sum(i,j);
int m3=sum(j,n-1);
if(m2>m3&&m2%3==0&&m==m1+m2/3)
{
asw++;
}
}
}
}
void DFS(int start,int n,int m)
{
if (start==n)//表示全排列完成
{
Found(a,n,m);
}
else
{
for (int i = 1; i <10 ; ++i) {
if(flag[i])//如果没有搜索过
{
continue;//对于以这个开头的数
a[start]=i;
flag[i]=1;
DFS(start+1,n,m);
flag[i]=0;//重置,让后一个开头的数能够循环
}
}
}
}
int main()
{
int i ,j,m;
double s1,s2;
fill(flag,flag+10,0);
cin>>m;
DFS(1,10,m);//1-9进行全排列
cout<<m<<' '<<asw;
return 0;
}非递归实现组合型枚举
链接:https://ac.nowcoder.com/acm/problem/50925
来源:牛客网题目描述
从 1~n 这 n 个整数中随机选出 m 个,输出所有可能的选择方案。n>0n \gt 0n>0, 0≤m≤n0 \leq m \leq n0≤m≤n, n+(n−m)≤25n+(n-m)\leq 25n+(n−m)≤25。
输入描述:
两个整数n,m。输出描述:
按照从小到大的顺序输出所有方案,每行1个。首先,同一行内的数升序排列,相邻两个数用一个空格隔开。其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面(例如1 3 9 12排在1 3 10 11前面)。示例1
输入
5 3输出
1 2 3 1 2 4 1 2 5 1 3 4 1 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5
#include<bits/stdc++.h>
using namespace std;
int sz[100];
int n,m;
void dfs(int pos,int val)
{
if(pos==m)
{
cout<<sz[0];
for(int i=1; i<pos; i++)
cout<<" "<<sz[i];
cout<<endl;
return ;
}
for(int i=val+1; i<=n; i++)
{
sz[pos]=i;
dfs(pos+1,i);
}
}
int main()
{
cin>>n>>m;
if(m==0)
cout<<endl;
else if(m==1)
{
for(int i=1; i<=n; i++)
cout<<i<<endl;
}
else
{
for(int i=1; i<=n; i++)
{
sz[0]=i;//记录数组
dfs(1,sz[0]);
}
}
return 0;
}费解的开关
链接:https://ac.nowcoder.com/acm/problem/50920
来源:牛客网你玩过“拉灯”游戏吗?25盏灯排成一个5x5的方形。每一个灯都有一个开关,游戏者可以改变它的状态。每一步,游戏者可以改变某一个灯的状态。游戏者改变一个灯的状态会产生连锁反应:和这个灯上下左右相邻的灯也要相应地改变其状态。
我们用数字“1”表示一盏开着的灯,用数字“0”表示关着的灯。下面这种状态
10111
01101
10111
10000
11011在改变了最左上角的灯的状态后将变成:
01111
11101
10111
10000
11011再改变它正中间的灯后状态将变成:
01111
11001
11001
10100
11011给定一些游戏的初始状态,编写程序判断游戏者是否可能在6步以内使所有的灯都变亮。
输入描述:
第一行有一个正整数n,代表数据中共有n个待解决的游戏初始状态。 以下若干行数据分为n组,每组数据有5行,每行5个字符。每组数据描述了一个游戏的初始状态。各组数据间用一个空行分隔。 对于30%的数据,n≤5n \leq 5n≤5; 对于100%的数据,n≤500n \leq 500n≤500。输出描述:
输出数据一共有n行,每行有一个小于等于6的整数,它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。 对于某一个游戏初始状态,若6步以内无法使所有灯变亮,请输出“-1”。示例1
输入
3 00111 01011 10001 11010 11100 11101 11101 11110 11111 11111 01111 11111 11111 11111 11111输出
3 2 -1
说明改变一盏灯后
其上下左右十字形区域将会都取反
注意以下:
- 所有问题的最后的方案取决于第一行的初态,
- 所以列举第一行32种初态,进行改变
- 然后像解cube一样,一行行地进行消除,变成灯全开的状态
- 每一行灯全开依赖于下一行的同列
- 最后最后一行不能由下一行进行啊改变
- 所以最后一行如果是全开的话 ,就有解,如果最后一行不是全开的话就无解,换而言之只用判断最后一行状态就行
- 由于题目大小限制所以建议使用位运算进行操作
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int INF = 0x3f3f3f3f;
char mp[7][7];
int dx[5] = { 0,0,-1,1,0 }, dy[5] = { 1,-1,0,0,0 };//方位数组
void turn(int x, int y)//使坐标(x,y)周围的灯的状态改变
{
for (int i = 0;i < 5;i++)
{
int a = x + dx[i];
int b = y + dy[i];
if (a >= 0 && a < 5 && b >= 0 && b < 5)//如果没有出边界
mp[a][b] = '0' + '1' - mp[a][b];//使满足条件的灯的状态改变
}
}
int work()
{
int res = INF;
for (int k = 0;k < (1 << 5);k++)//第0行***有5个灯,每个灯都有按与不按两种选择,对应于k的2进制表示就是每位上的1/0。所以最后共有32种情况。我们将第一行所有按的情况都枚举一下,在第一行确定的情况下,剩下的行数,按与不按也就可以确定了(1往后移动5位,表示2的5次方)1*2次方
{
char re[7][7];
int ans = 0;
memcpy(re, mp, sizeof (mp));//把mp中的信息拷贝到re中
for (int i = 0;i < 5;i++)
if (k >> i & 1)//对于第一行的i个等,如果这个灯是开的
{
ans++;
turn(0, i);//根据k的2进制表示信息我们可以知道需要将(0,i)上的灯按一下
}
for (int i = 0;i < 4;i++)//对于1-4行的灯,其状态都由第一行决定
{
for (int j = 0;j < 5;j++)
if (mp[i][j] == '0')//如果这一行的为0,按下一行同列的灯来改变,一行一行的进行消除
{
ans++;
turn(i + 1, j);
}
}
bool is_sucessful = true;//之后只有最后一行会产生错误,判断最后一行的灯是不是全部都是亮的,如果是的话就表示我们枚举的这个方案是成功的
for (int i = 0;i < 5;i++)
if (mp[4][i] == '0')
{
is_sucessful = false;
break;
}
if (is_sucessful)//如果该方案成功的话我们需要维护一下最小值便于最后输出方案最小值
res = min(res, ans);
memcpy(mp, re, sizeof (mp));//再把mp中灯的开关情况恢复,便于接下来对k的枚举
}
if(res>6)
res=-1;
return res;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n;
cin >> n;
while (n--)
{
for (int i = 0;i < 5;i++)
{
for (int j = 0;j < 5;j++)
cin >> mp[i][j];
}
cout << work() << endl;
}
return 0;
}汉诺塔问问题
链接:https://ac.nowcoder.com/acm/problem/50921
来源:牛客网译文描述
背景查理·黑褐色(Charlie Darkbrown)参加了另一门无聊的计算机科学课程:目前,老师只是在解释河内塔的标准问题,这使查理感到无聊! 老师指着黑板(图4)说:“所以这是问题所在:
一共有三座塔楼:A,B和C。
有n个磁盘。拼图游戏时,数字n是恒定的。
所有磁盘的大小均不同。
磁盘最初堆叠在塔A上,其大小从顶部到底部逐渐增加。
难题的目标是将所有磁盘从塔A转移到塔C。
一次可以将一个磁盘从塔架顶部移动到空塔架或顶部具有更大磁盘的塔架上。
因此,您的任务是编写一个程序,以计算将所有磁盘从A塔移动到C所需的最小磁盘移动次数。”
Charlie:“这非常无聊,每个人都知道可以使用简单的递归来解决。拒绝编写像这样简单的代码!”
老师叹了口气:“好吧,查理,让我们考虑一下要为您做的事情:为您提供第四塔D。计算最小数量的磁盘移动以移动所有磁盘。塔A到D都使用了全部四个塔。”
查理看上去很生气:“嗯。。。好吧,我不知道四塔的最佳算法。。。“
问题
因此,真正的问题是解决问题不属于查理擅长的事情。实际上,查理唯一真正擅长的就是“坐在可以做这项工作的人旁边”。现在,猜猜是什么-完全是!坐在查理旁边的是你,他已经瞪着你。
幸运的是,您知道以下算法适用于n <= 12:首先固定塔A上的k> = 1个磁盘,然后使用四个塔的算法将剩余的nk个磁盘从塔A移至塔B.使用三个塔的算法,将k个塔中的k个磁盘移到塔D中。最后,使用用于四个塔的算法,将塔B中的n-k个磁盘再次移动到塔D中(从而不移动塔D上已有的k个磁盘中的任何一个)。对所有k 2∈{1,….,n}执行此操作,并找到移动次数最少的k。
因此,对于n = 3和k = 2,您首先需要使用四塔算法(一次移动)将1(3-2)个磁盘从塔A移到塔B。然后,您将使用三个塔的算法将剩余的两个磁盘从塔A移到塔D(三步)。最后一步是再次使用四个塔的算法将磁盘从塔B移到塔D(另一个移动)。因此,对于n = 3和k = 2的解是5个移动。为确保这确实是n = 3的最佳解决方案,您需要检查k的其他可能值1和3。(但是,顺便说一句,5是最佳的。。。)输入描述:
没有输入。输出描述:
对于每个n(1 <= n <= 12),请打印一行以包含最少移动次数,以解决四个塔和n个磁盘的问题。
采用动态规划
week 2
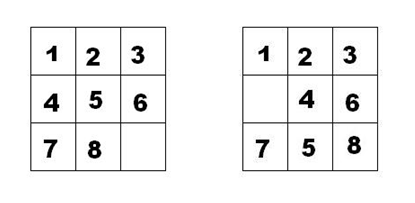
九宫重排
题目 1426: [蓝桥杯][历届试题]九宫重排
时间限制: 1Sec 内存限制: 128MB 提交: 3297 解决: 955
题目描述
如下面第一个图的九宫格中,放着 1~8 的数字卡片,还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动,可以形成第二个图所示的局面。
我们把第一个图的局面记为:12345678.
把第二个图的局面记为:123.46758
显然是按从上到下,从左到右的顺序记录数字,空格记为句点。
本题目的任务是已知九宫的初态和终态,求最少经过多少步的移动可以到达。如果无论多少步都无法到达,则输出-1。输入
输入第一行包含九宫的初态,第二行包含九宫的终态。
输出
输出最少的步数,如果不存在方案,则输出-1。
样例输入
12345678. 123.46758样例输出
3
#include <iostream>
#include <queue>
#include <map>
#include <algorithm>
#include <algorithm>
using namespace std;
string first,last,string1,string2;
int flag,x,y;
map<string,int> dis,vis;
queue<string> q1,q2;
char a[3][3];
const int dir[4][2]={{0,1},{0,-1},{1,1},{-1,-1}};
int ans;
bool isIn(int x,int y)
{
return (x>=0&&x<=3&&y<=3&&y>=0);
}
void toMatrix(string str)
{
for (int i = 0; i <9 ; ++i) {
a[i/3][i%3]=str[i];
}
}
string toString()
{
string str;
for (int i = 0; i < 9; ++i) {
str.push_back(a[i/3][i%3]);
}
return str;
}
int bfs()
{
q1.push(first);
dis[first]=1;
vis[first]=1;
q2.push(last);
dis[last]=1;
vis[last]=2;
while (!q1.empty()&&!q2.empty())
{
if (q1.size()<q2.size())
{
string1=q1.front();
q1.pop();
flag=1;
} else{
string1=q2.front();
q2.pop();
flag=2;
}
toMatrix(string1);
for (int i = 0; i <9; ++i) {
if(a[i/3][i%3]=='.')
{
x=i/3;
y=i%3;
}
}
for (int i = 0; i <4 ; ++i) {
int tx=x+dir[i][0];
int ty=y+dir[i][1];
if (isIn(tx,ty))
{
swap(a[x][y],a[tx][ty]);
//改变数组;
string2=toString();
//产生新的状态
if(!dis.count(string2))//如果没有访问过
{
dis[string2]=dis[string1]+1;//次态等于初态加一
vis[string2]=vis[string1];//记录由上一个继承而来
if(flag==1)
q1.push(string2);
if (flag==2)
q2.push(string2);
}
else
{//如果访问过
if (vis[string1]+vis[string2]==3)//如果重合,那么1达到的次态二的初态也能达到
{
ans=dis[string1]+dis[string2]-1;//注意有减一
return ans;
}
}
swap(a[x][y],a[tx][ty]);//注意转回初态
}
}
}
return -1;
}
int main()
{
cin>>first>>last;
if (first==last)
cout<<0;
else
cout<<bfs()<<endl;
return 0;
}random蚂蚁
题目 1429: [蓝桥杯][2014年第五届真题]兰顿蚂蚁
时间限制: 1Sec 内存限制: 128MB 提交: 3824 解决: 1716
题目描述
兰顿蚂蚁,是于1986年,由克里斯·兰顿提出来的,属于细胞自动机的一种。
平面上的正方形格子被填上黑色或白色。在其中一格正方形内有一只“蚂蚁”。
蚂蚁的头部朝向为:上下左右其中一方。蚂蚁的移动规则十分简单:
若蚂蚁在黑格,右转90度,将该格改为白格,并向前移一格;
若蚂蚁在白格,左转90度,将该格改为黑格,并向前移一格。规则虽然简单,蚂蚁的行为却十分复杂。刚刚开始时留下的路线都会有接近对称,像是会重复,但不论起始状态如何,蚂蚁经过漫长的混乱活动后,会开辟出一条规则的“高速公路”。
蚂蚁的路线是很难事先预测的。
你的任务是根据初始状态,用计算机模拟兰顿蚂蚁在第n步行走后所处的位置。
输入
输入数据的第一行是 m n 两个整数(3 < m, n < 100),表示正方形格子的行数和列数。
接下来是 m 行数据。
每行数据为 n 个被空格分开的数字。0 表示白格,1 表示黑格。接下来是一行数据:x y s k, 其中x y为整数,表示蚂蚁所在行号和列号(行号从上到下增长,列号从左到右增长,都是从0开始编号)。s 是一个大写字母,表示蚂蚁头的朝向,我们约定:上下左右分别用:UDLR表示。k 表示蚂蚁走的步数。
输出
输出数据为一个空格分开的整数 p q, 分别表示蚂蚁在k步后,所处格子的行号和列号。
样例输入
5 6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 3 L 5样例输出
1 3
#include <iostream>
#include <string>
using namespace std;
typedef struct {
int x;
int y;
int dict;
}ant;
string a="ULDR";//逆时针顺序,黑色加1,白色减1
int dict[4][2]={{0,-1},{-1,0},{0,1},{1,0}};
int MAP[20][100]={0};
int K;
int n,m;
char d;
int main()
{
ant an;
cin>>m>>n;
for (int i=1;i<=m;i++)
for (int j = 1; j <=n ; ++j) {
cin>>MAP[i][j];
}
cin>>an.x>>an.y>>d>>K;
an.dict=a.find(d);
cout<<an.dict<<endl;
while (K--)
{
if (MAP[an.x][an.y])//如果是黑色的地区是话
{
MAP[an.x][an.y]=0;
an.dict=(an.dict+1)%4;
an.y+=dict[an.dict][0];
an.x+=dict[an.dict][1];
}
else//如果是白色的地区的话
{
MAP[an.x][an.y]=1;//改变颜色
if (an.dict==0)
an.dict=3;
else
an.dict--;//改变方向
an.y+=dict[an.dict][0];
an.x+=dict[an.dict][1];//改变位置
}
}
cout<<an.x<<' '<<an.y<<' '<<endl;
return 0;
}剪格子
题目 1432: [蓝桥杯][2013年第四届真题]剪格子
时间限制: 1Sec 内存限制: 128MB 提交: 3196 解决: 1106
题目描述
历届试题 剪格子
时间限制:1.0s 内存限制:256.0MB问题描述
如下图所示,3 x 3 的格子中填写了一些整数。
+––+–+
|10 1|52|
+––+
|20|30* 1|
***–+
| 1| 2| 3|
+–+–+–+
我们沿着图中的星号线剪开,得到两个部分,每个部分的数字和都是60。
本题的要求就是请你编程判定:对给定的m x n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。
如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割,则输出 0。输入
程序先读入两个整数 m n 用空格分割 (m,n< 10)。
表示表格的宽度和高度。
接下来是n行,每行m个正整数,用空格分开。每个整数不大于10000。输出
输出一个整数,表示在所有解中,包含左上角的分割区可能包含的最小的格子数目。
样例输入
3 3 10 1 52 20 30 1 1 2 3样例输出
3
#include <iostream>
using namespace std;
int map_[11][11];
using namespace std;
int ans=1;
int goal=0;
int dic[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
int tx,ty;
int visited[10][10];
int m,n;
void dfs(int x,int y,int total,int cnt)
{
if (total==goal)
{
ans<cnt?ans:cnt;
return;
}
if (total>goal)
return;
else
{
for (auto & i : dic) {
tx=x+i[0];
ty=y+i[1];
if (tx>=0&&tx<=m&&ty>=0&&ty<=n&&!visited[ty][tx])
{
total+=map_[ty][tx];
cnt++;
visited[ty][tx]= 1;
dfs(tx,ty,total,cnt);
visited[ty][tx]=0;
} else
{
continue;
}
}
}
}
int main()
{
cin>>m>>n;
fill(visited,visited+10*10,0);//访问数组初始化
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
cin>>map_[i][j];
goal+=map_[i][j];
}
}
goal=goal/2;
dfs(0,0,map_[0][0],1);
return 0;
}蓝桥杯第十一届真题
既约分数

#include<iostream>
using namespace std;
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
int main()
{
int sum = 0;
//分子分母相同的情况
sum = 1;
int sum2 = 0;
//分子小于分母的情况
for(int i = 1; i < 2020; i++)
{
for(int j = i + 1; j <= 2020; j++)
{
if(gcd(i, j) == 1)
{
sum2++;
}
}
}
sum += sum2 * 2;
cout << sum << endl;
return 0;
}
def fun(a,b):
if a%b:
return fun(b,a%b)
else:
return b
total=0
for i in range(1,2020):
for j in range(1,2021):
if fun(i,j)==1:
total+=1
print(total)#注意以上C++写法不对,要加1蛇形填数
题目
试题 C: 蛇形填数
本题总分:10 分【问题描述】
如下图所示,小明用从 1 开始的正整数“蛇形”填充无限大的矩阵。
1 2 6 7 15 …
3 5 8 14 …
4 9 13 …
10 12 …
11 …
…容易看出矩阵第二行第二列中的数是 5。请你计算矩阵中第 20 行第 20 列的数是多少?
#include<bits/stdc++.h>
using namespace std;
int main()
{
int s,t=0,sum=0;
s=2*20-1; // 根据等差数列计算出第二十行二十列是第几条对角线
for(int i=1;i<=s-1;i++) // 计算前38条对角线数字之和
{
t++;
sum+=t;
}
s=s/2+1; // 第39条对角线上属于范围内的数字之和
sum+=s;
cout<<sum;
} #蛇形填数
def func(x):
if x == 1:
return 1
elif x == 2:
return 5
else:
return func(x - 1) + 4 * (x - 1)
print(func(20))
七段码

#include<bits/stdc++.h>
using namespace std;
const int N=10;
int use[N],ans,e[N][N],fa[N];
void init(){
//连边建图,e[i][j]==1表示i和j相邻
//a b c d e f g
//1 2 3 4 5 6 7
e[1][2]=e[1][6]=1;
e[2][1]=e[2][7]=e[2][3]=1;
e[3][2]=e[3][4]=e[3][7]=1;
e[4][3]=e[4][5]=1;
e[5][4]=e[5][6]=e[5][7]=1;
e[6][1]=e[6][5]=e[6][7]=1;
}
int find(int u){if(fa[u]==u)return u;fa[u]=find(fa[u]);return fa[u];}//并查集
void dfs(int d){
if(d>7){
/* 并查集判联通 */
for(int i=1;i<=7;i++)fa[i]=i;
for(int i=1;i<=7;i++)
for(int j=1;j<=7;j++)
if(e[i][j]&&use[i]&&use[j]){
int fx=find(i),fy=find(j);
if(fx!=fy){
fa[fx]=fy;
}
}
int k=0;
for(int i=1;i<=7;i++)if(use[i]&&fa[i]==i)k++;
if(k==1)ans++;
return;
}
use[d]=1;//打开d这个灯,继续开关下一个灯
dfs(d+1);
use[d]=0;//关闭d这个灯,继续开关下一个灯
dfs(d+1);
}
int main(){
init();
dfs(1);
cout<<ans;
}import numpy as np
import itertools as it
class UnionFind:
def __init__(self, n):
self.father = list(range(n))
self.size = [1] * n
# 当前连通分量数目
self.setCount = n
def find(self, x):
if self.father[x] == x:
return x
self.father[x] = self.find(self.father[x])
return self.father[x]
def merge(self, x, y):
x, y = self.find(x), self.find(y)
if x == y:
return False
if self.size[x] < self.size[y]:
x, y = y, x
self.father[y] = x
self.size[x] += self.size[y]
self.setCount -= 1
return True
res = 0
data = list(np.zeros((7, 7)))
data[0][1] = data[0][5] = 1
data[1][0] = data[1][6] = data[1][2] = 1
data[2][1] = data[2][3] = data[2][6] = 1
data[3][2] = data[3][4] = 1
data[4][3] = data[4][5] = data[4][6] = 1
data[5][0] = data[5][4] = data[5][6] = 1
num = [i for i in range(0, 7)]
for i in range(1, 8):
total = it.combinations(num, i)
for j in total:
uf = UnionFind(7)
for z in j:
for k in range(len(data[z])):
z = int(z)
b = int(data[z][k])
if b == 1 and k in j:
uf.merge(z, k)
if uf.setCount == 7 - len(j) + 1:
res += 1
print(res)成绩分析

太简单就不贴代码了
回文日期

#include <cstring>
#include <iostream>
using namespace std;
int days[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
bool check(int date)
{
int year = date / 10000;
int mouth = (date / 100) % 100;
int day = date % 100;
if(mouth < 0 || mouth > 12) return false;
if(day == 0 || mouth != 2 && day > days[mouth]) return false;
if(mouth == 2)
{
int leap = year % 100 && year % 4 == 0 || year % 400 == 0;
if(day > days[mouth] + leap) return false;
}
return true;
}
int main()
{
int date1, date2;
cin >> date1 >> date2;
int res = 0;
for(int i = 1000; i < 10000; i ++)
{
int date = i, x = i;
for(int j = 0; j < 4; j ++ ) date = date * 10 + x % 10, x /= 10;
if(date1 <= date && date <= date2 && check(date)) res ++;
}
cout << res << endl;
return 0;
}子串分值


#include <iostream>
#include <cstring>
using namespace std;
int flag[26];
int num;
int main()
{
string str;
cin >> str;
long long sum = 0;
for(int i = 0; i < str.length(); ++i){
for(int j = i; j < str.length(); ++j){
flag[str[j] - 'a']++;
if(flag[str[j] - 'a'] == 1){
num++;
}
sum += num;
}
memset(flag, 0, sizeof(flag));
num = 0;
}
cout << sum << '\n';
return 0;
}字串排序

DP
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 135, M = 10010;
int f[N][30][N];
//chcnt[i][j]记录第i个位置取字母j+'a'的逆序对最大值
int chcnt[N][30];
//mlen[i]记录每个位置的最大值
int mlen[N];
void dp()
{
for (int i = 2; i < N; ++i)
{
int m = 0;
for (int j = 1; j <= 'z' - 'a'; ++j)
{
for (int k = 1; k < i; ++k)
{
if (k > 1) f[i][j][k] = f[i - 1][j][k - 1] + i - k;
else f[i][j][k] = chcnt[i - 1][j - 1] + i - 1;
chcnt[i][j] = max(chcnt[i][j], f[i][j][k]);
}
m = max(m, chcnt[i][j]);
}
mlen[i] = m;
}
}
int main()
{
dp();
int score = 0;
cin >> score;
//找出最短长度值
int beg = 0;
for (int i = 1; i < N; ++i)
if (mlen[i] >= score)
{
beg = i;
break;
}
int curr = 0; //用于记录逆序值
int same = 1; //记录后缀中有多少个相同字母
char last = 'z' + 1;//记录上一个字母是什么
for (int i = beg; i > 0; --i)
{
//从a开始枚举
int j = 0;
for (; j <= last - 'a'; ++j)
{
if (j == last - 'a') curr -= same;
if (curr + chcnt[i][j] >= score)
{
curr += i - 1;
break;
}
}
if (j == last - 'a') same++;
else
{
last = j + 'a';
same = 1;
}
cout << last;
}
cout << endl;
return 0;
}蓝桥杯第十届
平方和

数列求和

#include<bits/stdc++.h>
using namespace std;
int main(){
int a[4]={1,1,1};
int s = 0;
for(int i = 4;i<=20190324;i++){
s = a[0]+a[1]+a[2];
s = s%10000;
a[0]=a[1];
a[1]=a[2];
a[2]=s;
// cout<<a[2]<<endl;
}
cout<<a[2]<<endl;
return 0;
}最大降雨量

34
证明:无法找到比34更优的方案了。如下图,假设每周选的数已经排好序
第一周: x x x x x x x ( x1,x2,x3,x4,x5,x6 满足 x1<x2<x3<x4<x5<x6)
第二周: x x x x x x x
第三周: x x x x x x x
第四周: x x x x x x x
第五周: x x x x x x x
第六周: x x x x x x x
第七周: x x x x x x x
则标记红色的是每周的中位数:
第一周: x x x x x x x
第二周: x x x x x x x
第三周: x x x x x x x
第四周: x x x x x x x
第五周: x x x x x x x
第六周: x x x x x x x
第七周: x x x x x x x
此时不看第几周,每一行里:红色的x右边的x必然比x大。
假设上面的七行按行按照x由小到大重新排序后得到
x x x x1 x x x
x x x x2 x x x
x x x x3 x x x
x x x x4 x x x
x x x x5 x x x
x x x x6 x x x
x x x x7 x x x
则x1<x2<x3<x4<x5<x6<x7 题目要求的中位数的中位数就是x4了
问题是x4最大能取到多少呢?注意到上图中x4右下角(如下图)的元素都应比x4大。。(共15个)
因此答案为49-15=34
x x x x x x x
x x x x x x x
x x x x x x x
x x x x4 x x x
x x x x x x x
x x x x x x x
x x x x x x x
————————————————
原文链接:https://blog.csdn.net/linruier2017/article/details/88803441
迷宫
bfs搜索即可
#include<queue>
#include<cstdio>
#include<string>
#include<cstring>
using namespace std;
char map[501][501]; //存成字符型
int vis[500][500];
/*
01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010101001000100010101
10100001000110010001000010101001110101011111010010
00000100101000000110010100101001100001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000
*/
int dir[4][2] = {
{1, 0}, //下
{0, -1}, //左
{0, 1}, //右
{-1, 0} //上
};
char dic[4]= {'D','L','R','U'};
struct node {
int x,y;
int step; //到达该节点的步数
string path; //到达该点路径
};
int x1,x2,y1,y2,n,m; //(x1,y1)起点,(x2,y2)终点
void bfs() {
queue<node> q;
node p; //当前所在的节点
p.x=x1;p.y=y1;p.step=0;p.path="";
vis[x1][y1]=1;
q.push(p);
while(!q.empty()){
node p=q.front(); //宽搜 队列待遍历节点
if(p.x==x2&&p.y==y2){
if(p.step==0){
}
cout<<p.step<<endl<<p.path;
}
node v; //下一步所要去往的节点
for(int i=0;i<4;i++){ //依次四个方向遍历
v.x=p.x+dir[i][0];
v.y=p.y+dir[i][1];
if(v.x>=0&&v.y>=0&&v.x<n&&v.y<m&&vis[v.x][v.y]==0&&map[v.x][v.y]!='1'){ //不能重复访问且走得通
vis[v.x][v.y]=1; //已访问
v.step=p.step+1;
v.path=p.path+dic[i];
q.push(v);
}
}
q.pop();
}
}
int main() {
n=30,m=50;
memset(map,'1',sizeof(map));
memset(vis,0,sizeof(vis));
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
cin>>map[i][j];
}
}
x1=0;y1=0;
x2=n-1;y2=m-1;
bfs();
return 0;
}完全二叉树权值
时间限制: 1.0s 内存限制: 256.0MB 本题总分:15 分
【问题描述】
给定一棵包含 N 个节点的完全二叉树,树上每个节点都有一个权值,按从上到下、从左到右的顺序依次是 A1, A2, · · · AN,如下图所示:
现在小明要把相同深度的节点的权值加在一起,他想知道哪个深度的节点权值之和最大?如果有多个深度的权值和同为最大,请你输出其中最小的深度。
注:根的深度是 1。
【输入格式】
第一行包含一个整数 N。
第二行包含 N 个整数 A1, A2, · · · AN 。
【输出格式】
输出一个整数代表答案。
【样例输入】
7
1 6 5 4 3 2 1【样例输出】
2【评测用例规模与约定】
对于所有评测用例,1 ≤ N ≤ 100000,−100000 ≤ Ai ≤ 100000
————————————————
原文链接:https://blog.csdn.net/linruier2017/article/details/88803441
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int a[100005];
int n;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
int level=1;//层数
ll MAX=a[1];
ll ans=1;//第一层
int num=1;//该层的节点数
int pos=2;//下一层开头指针位置
for(;;)
{
level++;
num*=2;
ll sum=0;
for(int j=pos;j<=min(pos+num-1,n);j++)sum+=a[j];
if(sum>MAX)
{
ans=level;
MAX=sum;
}
pos=pos+num;
if(pos>n)break;
}
printf("%lld\n",ans);
return 0;
}外卖店优先级



package JC2019;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int m=sc.nextInt();
int t=sc.nextInt();
HashMap<Integer,Integer> arr[]=new HashMap[t+1];
for(int i=0;i<t+1;i++){
arr[i]=new HashMap<Integer,Integer>();
}
int id,ti;
for(int i=0;i<m;i++){
ti=sc.nextInt();
id=sc.nextInt();
if(arr[ti].containsKey(id)){
arr[ti].put(id, arr[ti].get(id)+1);
}else{
arr[ti].put(id, 1);
}
}
int last[]=new int[n+1];
int scor[]=new int[n+1];
int prio[]=new int[n+1];
for(int i=0;i<=t;i++){
for(int temp:arr[i].keySet()){
scor[temp]=Math.max(scor[temp]-(i-last[temp]-1),0);
if(scor[temp]>5&&prio[temp]==0){
prio[temp]=1;
}else if(scor[temp]<4&&prio[temp]==1){
prio[temp]=0;
}
scor[temp]+=arr[i].get(temp)*2;
if(scor[temp]>5&&prio[temp]==0){
prio[temp]=1;
}
last[temp]=i;
}
}
for(int i=0;i<=n;i++){
scor[i]=Math.max(scor[i]-(t-last[i]),0);
if(scor[i]<4&&prio[i]==1){
prio[i]=0;
}
}
int ans=0;
for(int i=0;i<=n;i++){
ans+=prio[i];
}
System.out.println(ans);
}
}修改数组
时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
【问题描述】
给定一个长度为 N 的数组 A = [A1, A2, · · · AN],数组中有可能有重复出现的整数。
现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改
A2, A3, · · · , AN。
当修改 Ai 时,小明会检查 Ai 是否在 A1 ∼ Ai−1 中出现过。如果出现过,则小明会给 Ai 加上 1 ;如果新的 Ai 仍在之前出现过,小明会持续给 Ai 加 1 ,直到 Ai 没有在 A1 ∼ Ai−1 中出现过。
当 AN 也经过上述修改之后,显然 A 数组中就没有重复的整数了。现在给定初始的 A 数组,请你计算出最终的 A 数组。
【输入格式】
第一行包含一个整数 N。
第二行包含 N 个整数 A1, A2, · · · , AN 。
【输出格式】
输出 N 个整数,依次是最终的 A1, A2, · · · , AN。
【样例输入】
5
2 1 1 3 4【样例输出】
2 1 3 4 5【评测用例规模与约定】
对于 80% 的评测用例,1 ≤ N ≤ 10000。
对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ Ai ≤ 1000000。
————————————————
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int bit[2000050];
int n=1000001;
int sum(int i)
{
int s=0;
while(i>0)
{
s+=bit[i];
i-=i&-i;
}
return s;
}
void add(int i,int x)
{
while(i<=n)
{
bit[i]+=x;
i+=i&-i;
}
}
bool ok(int k,int pre)
{
int l=k-pre+1;
int cnt=sum(k)-sum(pre-1);
return cnt<l;
}
bool vis[1000005];
int ans[100005];
int N;
int a[100005];
int main()
{
scanf("%d",&N);
for(int i=0;i<N;i++)scanf("%d",&a[i]);
for(int i=0;i<N;i++)
{
if(!vis[a[i]])
{
ans[i]=a[i];
vis[a[i]]=1;
add(a[i],1);
}
else {
int l=a[i];int r=1000002;
int mid;
while(r-l>1)
{
mid=(l+r)/2;
if(ok(mid,a[i]))r=mid;
else l=mid;
}
ans[i]=r;
vis[r]=1;
add(r,1);
}
}
for(int i=0;i<N;i++)printf("%d%c",ans[i],i==N-1?'\n':' ');
return 0;
}糖果
糖果店的老板一共有 M 种口味的糖果出售。为了方便描述,我们将 M 种口味编号 1 ∼ M。
小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果,而 是 K 颗一包整包出售。
幸好糖果包装上注明了其中 K 颗糖果的口味,所以小明可以在买之前就知道每包内的糖果口味。
给定 N 包糖果,请你计算小明最少买几包,就可以品尝到所有口味的糖果。【输入格式】
第一行包含三个整数 N、M 和 K。
接下来 N 行每行 K 这整数 T1, T2, · · · , TK,代表一包糖果的口味。
【输出格式】
一个整数表示答案。如果小明无法品尝所有口味,输出 −1。
【样例输入】
6 5 3
1 1 2
1 2 3
1 1 3
2 3 5
5 4 2
5 1 2【样例输出】
2【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ N ≤ 20 。
对于所有评测样例,1 ≤ N ≤ 100,1 ≤ M ≤ 20,1 ≤ K ≤ 20,1 ≤ Ti ≤ M。
#include<bits/stdc++.h>
using namespace std;
int dp[1000005];
int n,m,k;
int s[105];//代表第i包糖果
int main()
{
memset(dp,-1,sizeof(dp));
scanf("%d%d%d",&n,&m,&k);
for(int i=0;i<n;i++)
{
int ss=0;
int t;
for(int j=0;j<k;j++)
{
scanf("%d",&t);
ss|=(1<<(t-1));
}
s[i]=ss;
dp[ss]=1;
}
for(int i=0;i<n;i++)
{
for(int j=0;j<(1<<m);j++)
{
if(dp[j]==-1)continue;
if(dp[j|s[i]]==-1)dp[j|s[i]]=dp[j]+dp[s[i]];
else dp[j|s[i]]=min(dp[j|s[i]],dp[j]+dp[s[i]]);
}
}
printf("%d\n",dp[(1<<m)-1]);
return 0;
}组合数问题
弃疗弃疗了